D(demand) qd | Schedule P |
| 10 | 0 |
| 8 | 1 |
| 4 | 2 |
| 1 | 3 |
| 0 | 4 |
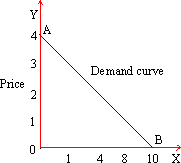
(A) Demand Schedule : The various quantities demanded of a particular commodity are presented here in a schedule. At arbitrarily chosen prices, the quantity of a commodity an individual consumer is expected to demand, is explained by the schedule. Since quantity demanded (qd) depends on the relevant prices of goods, the two can be expressed in the form of an algebraic function as well. The schedule shows that as price goes on rising (from zero to 4) the quantity demanded goes on falling (from 10 to zero).
The scheduled information has been presented in the form of a demand curve in Figure 2 (below). In the figure, the units of quantity of the goods have been measured along the horizontal axis (OX) and the respective prices have been shown along the vertical axis (OY). The curve intersects OY axis at point A which shows highest price at which quantity demanded is zero. On the contrary the curve intersects OX axis at point B showing largest quantity demanded where price is zero. Both OA and OB are said to be intercept quantities when one of the variables assumes zero value. Note that demand curve is sloping downward. This follows the law of demand (given below). But the demand curve of such a shape is obvious from the fact that quantities demanded and price in the demand schedule hold an inverse relationship.
Quantity Demanded qd
Figure 2
(B) Demand Function: The price-demand relationship shown above can be expressed in the form of a demand function as follows:
qd = 10 - 3P
On substitution of any scheduled value of P we get the relevant value of the quantity demanded. Thus when P = 1 then qd =10 - 3 (1) = 7 or when P = 3, then qd = 10 - 3 (3) = 1 etc.
(C) Law of demand: The law of demand explains the inverse relation between quantity and price in general. It can be stated as follows:
"Ceteris Paribus (other things remaining equal), the quantity of a good demanded will rise (expand) with every fall in its price and the quantity of a good demanded will fall (contract) with every rise in its price."
In a functional form this can be stated as,
qd = f (P) [ Y, Ps, N, Z ]const.
This explains that qd, the quantity of a good demanded functionally depends on its price P. However, the quantity demanded is also causally related to other factors such as income of an individual (Y), prices of substitutes (Ps), number of members in the family (N) and the tastes of the consumer (Z). In order to satisfy price-demand relation, the effect of these other variables has been restrained by assuming them to be constant.
Initially, the law of demand was based on the principle of diminishing marginal utility (DMU). But in that case it was implied that utility is cardinally or absolutely measurable. There were other practical difficulties in the DMU approach as well. Therefore recently attempts have been made to place the law of demand on the empirical and realistic basis. One such attempt is in the form of Indifference Curve (IC) analysis. Under the IC approach it is enough to measure utility in ordinal or relative terms.
(D) Rise or Fall and Increase or Decrease in demand: On a given demand curve as we move downwards from point A in the direction of B, the quantity demanded goes on rising with every successive fall in price. On the contrary, moving from point B to A shows a fall in the quantity demanded with every successive rise in the price. Marshall has called this process rise and fall or expansion and contraction in the demand. Therefore, in this case the price of the quantity (and the change in it) plays an important part. Here, a change in the quantity demanded is indicated with movement along the demand curve (up or down accordingly). This change is subject to the ceteris paribus condition.
On the other hand, other factors are also likely to alter the quantity demanded. This can be expressed by a shift in the curve. Such an upward shift in the demand curve (Figure 3) has been shown by a new and higher demand curve (A1B1) in the figure.
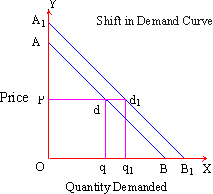
Figure 3
At a given price OP on the original demand curve (AB), the quantity demanded is Oq but on the new demand curve (A1B1) it has increased to Oq1. On the other hand, if we begin with the A1B1 demand curve as the initial demand curve and consider demand to have reduced (to AB) then the quantity demanded reduces from Oq1 to Oq. Such a change in the demand, arising out of a shift in the demand curve is known as an increase (if it is towards the right of the original demand curve) and a decrease (if it is towards the left of the original demand curve) in the demand, respectively.
The demand curve may shift and quantity demanded may increase or decrease, due to changes in a number of factors (apart from price), say the income (Y) of a consumer (when he becomes richer or poorer). A similar effect can be noticed with a rise or fall in the price of substitute (Ps) goods. For instance, tea and coffee or soaps of different brands are substitutes of each other. Therefore a rise in price of pasta may result in a reduction in the consumption of pasta and simultaneously an increase in the consumption of bread to that extent and vice versa. Or the demand curve may shift and quantity demanded may increase at the old price if there is a sudden increase in the number of members in a family (N), (say because of the unexpected arrival of guests). Finally, a shift in the demand curve may also be the result of the change in the tastes of a consumer. A cigarette or liquor consumer may become addicted because of which his demand for such goods will rise remarkably even at the old price.
There is an important difference between the change in the quantity demanded of a particular commodity and change in the demand for that commodity. While the former is influenced by the single factor: price, the latter is influenced by various other factors apart from price. A change in the quantity demanded is represented by a movement along the demand curve, while a change in the demand is represented by a shift of the curve (towards the left in case of a decrease and towards the right in case of an increase).
No comments:
Post a Comment